

Let's take a point P(rcosθ, rsinθ) on the boundary of the circle, where r is the distance of the point from the origin. We usually write the polar form of the equation of circle for the circle centered at the origin. The polar form of the equation of the circle is almost similar to the parametric form of the equation of circle. The parametric equation of circle can be written as x 2 + y 2 + 2hx + 2ky + C = 0 where x = -h + rcosθ and y = -k + rsinθ. The line joining this general point and the center of the circle (-h, -k) makes an angle of \(\theta\). We take a general point on the boundary of the circle, say (x, y). We know that the general form of the equation of a circle is x 2 + y 2 + 2hx + 2ky + C = 0. Squaring both sides, we get the standard form of the equation of the circle as:Ĭonsider this example of an equation of circle (x - 4) 2 + (y - 2) 2 = 36 is a circle centered at (4,2) with a radius of 6. Let's apply the distance formula between these points.
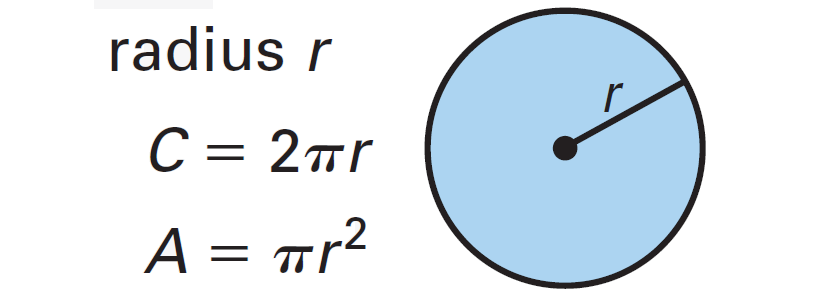
The distance between this point and the center is equal to the radius of the circle. The standard equation of a circle with center at \((x_1, y_1)\) and radius r is \( (x - x_1)^2 + (y - y_1)^2 = r^2\), where (x, y) is an arbitrary point on the circumference of the circle. The standard equation of a circle gives precise information about the center of the circle and its radius and therefore, it is much easier to read the center and the radius of the circle at a glance. So, we will be using the completing the square formula to make a quick conversion from the general form to the standard form.

Unlike the standard form which is easier to understand, the general form of the equation of a circle makes it difficult to find any meaningful properties about any given circle. This general form is used to find the coordinates of the center of the circle and the radius, where g, f, c are constants. The general form of the equation of a circle is: x 2 + y 2 + 2gx + 2fy + c = 0. Let's look at the two common forms of the equation of circle-general form and standard form of the equation of circle here along with the polar and parametric forms in detail. There are different forms to represent the equation of a circle, Using the equation of circle, once we find the coordinates of the center of the circle and its radius, we will be able to draw the circle on the cartesian plane. A circle can be drawn on a piece of paper given its center and the length of its radius. 1.Īn equation of circle represents the position of a circle on a cartesian plane. In this article, let's learn about the equation of the circle, its various forms with graphs and solved examples. A circle can be represented in many forms: Similarly, on a Cartesian plane, we can draw a circle if we know the coordinates of the center and its radius.
A circle can be drawn on a piece of paper if we know its center and the length of its radius. To represent a circle on the Cartesian plane, we require the equation of the circle. This equation is used across many problems of circles in coordinate geometry. The equation of a circle is different from the formulas that are used to calculate the area or the circumference of a circle. The equation of circle provides an algebraic way to describe a circle, given the center and the length of the radius of a circle.


 0 kommentar(er)
0 kommentar(er)
